机器学习 - 朴素贝叶斯分类器函数内容总结(sklearn)

1 贝叶斯分类器内容总结

1.1 各种概率分布有什么区别？

概率分布函数	特点
MultinomialNB（多项式分布）	适用于具有离散特征的分类（例如，用于文本分类的字数统计）。
GaussianNB（高斯分布）	假设特征的可能性(即概率)为高斯分布
BernoulliNB（伯努利分布）	像MultinomialNB一样，此分类器适用于离散数据。区别在于，虽然MultinomialNB可以处理出现次数，但BernoulliNB是为二进制/布尔功能而设计的。
ComplementNB（互补朴素贝叶斯）	ComplementNB的参数估计比MultinomialNB的参数估计更稳定。此外，ComplementNB在文本分类任务上的表现通常优于MultinomialNB（通常相当大）。
BayesianRidge（贝叶斯回归）	BayesianRidge可以用于再预估阶段的参数正则化。正则化参数的选择不是通过人为的选择，而是通过手动调节数据值来实现。

1.2 各种概率分布的参数怎么设置？

吐槽！！！！
Markdown这么多年了，竟然还不支持单元格合并，当然，可以使用HTML来解决这个问题，但我不想在我的Markdown里面插入过多的HTML元素，所以，丑就丑了，第一列我就不合并了！

概率分布函数	参数名	参数类型及默认值	参数描述
MultinomialNB（多项式分布）	alpha	Float类型，默认值为：1.0。	贝叶斯估计所添加的参数，alpha=1.0时，为拉普拉斯平滑。
	fit_prior	Bool类型，默认值为：True。	表示是否要学习先验概率，如果为False，则所有样本输出时使用统一的类别先验概率（1 / 类别数）。如果为True时，则可以利用第三个参数class_piror输入先验概率，或者不输入第三个参数，可以从训练集中自己计算先验概率，此时，第k个类别的先验概率=第k个类别样本数 / 总的样本数
	class_prior	List类型，默认值为None。	该类的先验概率。如果指定了先验，则不会根据数据进行调整。
GaussianNB（高斯分布）	priors	List类型，默认值为None。	该类的先验概率。如果指定，则先验数据不会根据数据进行调整。
	var_smoothing	Float类型，默认值为：1e-9。	所有特征的最大方差部分，已添加到方差中以提高计算稳定性。
BernoulliNB（伯努利分布）	alpha	Float类型，默认值为：1.0。	贝叶斯估计所添加的参数，alpha=1.0时，为拉普拉斯平滑。
	binarize	Float 或 None类型，默认值为：0.0。	用于将样本特征二值化（映射为布尔值）的阈值。如果为None，则假定输入已经由二进制向量组成。
	fit_prior	Bool类型，默认值为：True。	表示是否要学习先验概率，如果为False，则所有样本输出时使用统一的类别先验概率（1 / 类别数）。如果为True时，则可以利用第三个参数class_piror输入先验概率，或者不输入第三个参数，可以从训练集中自己计算先验概率。
	class_prior	List类型，默认值为None。	该类的先验概率。如果指定，则先验数据不会根据数据进行调整。
ComplementNB（互补朴素贝叶斯）	alpha	Float类型，默认值为：1.0。	贝叶斯估计所添加的参数，alpha=1.0时，为拉普拉斯平滑。
	fit_prior	Bool类型，默认值为：True。	表示是否要学习先验概率，如果为False，则所有样本输出时使用统一的类别先验概率（1 / 类别数）。如果为True时，则可以利用第三个参数class_piror输入先验概率，或者不输入第三个参数，可以从训练集中自己计算先验概率。
	class_prior	List类型，默认值为None。	该类的先验概率。如果指定，则先验数据不会根据数据进行调整。
	norm	Bool类型，默认值为：False。	是否执行权重的第二次标准化。
BayesianRidge（贝叶斯回归）	n_iter	Int类型，默认值为300。	最大迭代次数。应大于或等于1。
	tol	Float类型，默认值为：1e-3。	如果w已收敛，则停止算法。
	alpha_1	Float类型，默认值为：1e-6。	超参数：在alpha参数之前的Gamma分布的形状参数。
	alpha_2	Float类型，默认值为：1e-6。	超参数：反比例参数（速率参数）Gamma分布在alpha参数之前。
	lambda_1	Float类型，默认值为：1e-6。	超参数：在lambda参数之前的Gamma分布的形状参数。
	lambda_2	Float类型，默认值为：1e-6。	超参数：在lambda参数之前的Gamma分布的逆比例参数（速率参数）。
	alpha_init	Float类型，默认值为：None。	alpha的初始值（噪声的精度）。
	lambda_init	Float类型，默认值为：None。	lambda的初始值（权重的精度）。如果未设置，则lambda_init为1。
	compute_score	Bool类型，默认False。	如果为真，则在每次优化迭代时计算对数边际似然。
	fit_intercept	Bool类型，默认为True。	是否计算此模型的截距。截距不作为概率参数，因此没有相关的方差。如果设置为False，则计算中将不使用截距（即数据应居中）。
	normalize	Bool类型，默认值为：False。	当fit_intercept设置为False时，忽略此参数。如果为真，则回归前，通过减去平均值并除以l2范数，对回归数X进行归一化。
	copy_X	Bool类型，默认值为True。	如果为True，将复制X；否则，可能会覆盖它。
	verbose	Bool类型，默认值为False。	拟合模型时的详细模式。

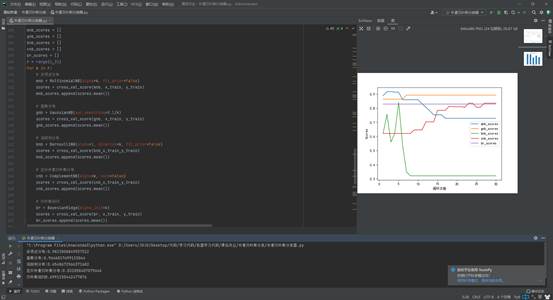
1.3 cross_val_score作用。

交叉验证的方法可以帮助我们进行调参，最终得到一组最佳的模型参数使得测试数据的准确率和泛化能力最佳。

如图所示，给出了5个概率分布函数，经过cross_val_score的图像。

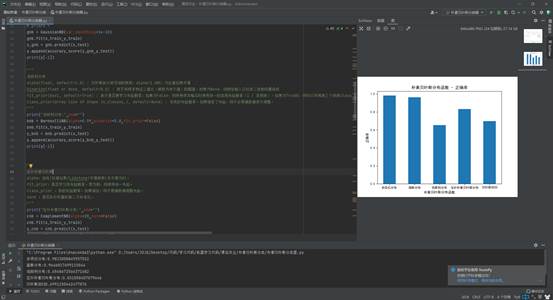
2 对比分析各种概率分布下鸢尾花分类正确率对比，并在一个柱形图上显示。

Out：

多项式分布:0.9823008849557522

高斯分布:0.9646017699115044

伯努利分布:0.6548672566371682

互补朴素贝叶斯分布:0.831858407079646

贝叶斯回归0.6991150442477876

3 代码实现

from matplotlib import pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split,cross_val_score
from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB
from sklearn.linear_model import BayesianRidge
import numpy as np
from sklearn.metrics import accuracy_score

y = []

iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target
# print(iris_x)
iris_x = iris_x[:,:]

# print(iris_y)
x_train,x_test,y_train,y_test = train_test_split(iris_x,iris_y,test_size=0.75,random_state=1)



"""
多项式分布
alpha (float, default=1.0):贝叶斯估计所添加的参数，alpha=1.0时，为拉普拉斯平滑
fit_prior(bool, default=True):表示是否要学习先验概率，如果为False，则所有样本输出时使用统一的类别先验概率（1 / 类别数）。如果为True时，则可以利用第三个参数class_piror输入先验概率，或者不输入第三个参数，可以从训练集中自己计算先验概率，此时，第k个类别的先验概率=第k个类别样本数 / 总的样本数
class_prior(array-like of shape (n_classes,), default=None):该类的先验概率。如果指定了先验，则不会根据数据进行调整。
"""
print("多项式分布:",end="")
mnb = MultinomialNB(alpha=0.01,fit_prior=False)
mnb.fit(x_train,y_train)
y_mnb = mnb.predict(x_test)
y.append(accuracy_score(y_mnb,y_test))
print(y[-1])

"""
高斯分布
priors(array-like of shape (n_classes,)) : 该类的先验概率。如果指定，则先验数据不会根据数据进行调整
var_smoothing(float, default=1e-9) : 所有特征的最大方差部分，已添加到方差中以提高计算稳定性。
"""
print("高斯分布:",end="")
# print(y_train)
# priors =
gnb = GaussianNB(var_smoothing=1e-10)
gnb.fit(x_train,y_train)
y_gnb = gnb.predict(x_test)
y.append(accuracy_score(y_gnb,y_test))
print(y[-1])

"""
伯努利分布
alpha(float, default=1.0) : 贝叶斯估计所添加的参数，alpha=1.0时，为拉普拉斯平滑
binarize(float or None, default=0.0) : 用于将样本特征二值化（映射为布尔值）的阈值。如果为None，则假定输入已经由二进制向量组成
fit_prior(bool, default=True) : 表示是否要学习先验概率，如果为False，则所有样本输出时使用统一的类别先验概率（1 / 类别数）。如果为True时，则可以利用第三个参数class_piror输入先验概率，或者不输入第三个参数，可以从训练集中自己计算先验概率，
class_prior(array-like of shape (n_classes,), default=None) : 该类的先验概率。如果指定了先验，则不会根据数据进行调整。
"""
print("伯努利分布:",end="")
bnb = BernoulliNB(alpha=0.99,binarize=5.8,fit_prior=False)
bnb.fit(x_train,y_train)
y_bnb = bnb.predict(x_test)
y.append(accuracy_score(y_bnb,y_test))
print(y[-1])


"""
互补朴素贝叶斯
alpha：加性(拉普拉斯/Lidstone)平滑参数(无平滑为0)。
fit_prior：是否学习类先验概率。若为假，则使用统一先验。
class_prior ：类的先验概率。如果指定，则不根据数据调整先验。
norm ：是否执行权重的第二次标准化。
"""
print("互补朴素贝叶斯分布:",end="")
cnb = ComplementNB(alpha=20,norm=False)
cnb.fit(x_train,y_train)
y_cnb = cnb.predict(x_test)
y.append(accuracy_score(y_cnb,y_test))
print(y[-1])

"""

"""
print("贝叶斯回归",end="")
br = BayesianRidge()

br.fit(x_train,y_train)
y_br = br.predict(x_test)
y_br = y_br.astype(np.int16)
y.append(accuracy_score(y_br,y_test))
print(y[-1])

"""
cross_val_score
estimator：数据对象
X：数据
y：预测数据
soring：调用的方法
cv：交叉验证生成器或可迭代的次数
n_jobs：同时工作的cpu个数（-1代表全部）
verbose：详细程度
fit_params：传递给估计器的拟合方法的参数
pre_dispatch：控制并行执行期间调度的作业数量。减少这个数量对于避免在CPU发送更多作业时CPU内存消耗的扩大是有用的。
"""

mnb_scores = []
gnb_scores = []
bnb_scores = []
cnb_scores = []
br_scores = []
r = range(1,31)
for k in r:
    # 多项式分布
    mnb = MultinomialNB(alpha=k, fit_prior=False)
    scores = cross_val_score(mnb, x_train, y_train)
    mnb_scores.append(scores.mean())

    # 高斯分布
    gnb = GaussianNB(var_smoothing=0.1/k)
    scores = cross_val_score(gnb, x_train, y_train)
    gnb_scores.append(scores.mean())

    # 伯努利分布
    bnb = BernoulliNB(alpha=1, binarize=k, fit_prior=False)
    scores = cross_val_score(bnb,x_train,y_train)
    bnb_scores.append(scores.mean())

    # 互补朴素贝叶斯分布
    cnb = ComplementNB(alpha=k, norm=False)
    scores = cross_val_score(cnb,x_train,y_train)
    cnb_scores.append(scores.mean())

    # 贝叶斯回归
    br = BayesianRidge(alpha_init=k)
    scores = cross_val_score(br, x_train, y_train)
    br_scores.append(scores.mean())


#解决中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

plt.plot(r, mnb_scores, label='mnb_scores')
plt.plot(r,gnb_scores,label='gnb_scores')
plt.plot(r, bnb_scores,label='bnb_scores')
plt.plot(r, cnb_scores,label='cnb_scores')
plt.plot(r, br_scores,label='br_scores')
plt.legend()
plt.xlabel("循环次数")
plt.ylabel("Scores")

plt.show()

x = ["多项式分布", "高斯分布", "伯努利分布", "互补朴素贝叶斯分布","贝叶斯回归"]




plt.bar(x,y,0.5)

plt.xlabel("朴素贝叶斯分布函数")
plt.xticks(fontsize=9)
plt.yticks(fontsize=9)
plt.ylabel("正确率")
plt.title("朴素贝叶斯分布函数 - 正确率")

plt.show()